Compact Manifolds with Special Holonomy (Oxford Mathematical Monographs)
by Dominic David Joyce
The book starts with a thorough introduction to connections and holonomy groups, and to Riemannian, complex and Kähler geometry. Then the Calabi conjecture is proved and used to deduce the existence of compact manifolds with holonomy SU(m) (Calabi-Yau manifolds) and Sp(m) (hyperkähler manifolds). These are constructed and studied using complex algebraic geometry. The second half of the book is devoted to constructions of compact 7- and 8-manifolds with the exceptional holonomy groups 92 and...
Non-Euclidean Geometries (Mathematics and Its Applications, #581)
by J nos Bolyai, A Pr kopa, and Emil Moln r
"From nothing I have created a new different world," wrote Janos Bolyai to his father, Wolgang Bolyai, on November 3, 1823, to let him know his discovery of non-Euclidean geometry, as we call it today. The results of Bolyai and the co-discoverer, the Russian Lobachevskii, changed the course of mathematics, opened the way for modern physical theories of the twentieth century, and had an impact on the history of human culture. The papers in this volume, which commemorates the 200th anniversary of...
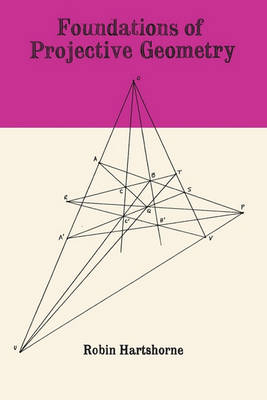
Vorlesungen uber Nicht-Euklidische Geometrie (Grundlehren der Mathematischen Wissenschaften, #26)
by Felix Klein
Als Felix Klein den Plan faBte, die wichtigsten seiner autogra- phierten Vorlesungen im Druck erscheinen zu lassen, gedachte er, mit der Nichteuklidischen Geometrie zu beginnen und den alten Text zu- vor mit Hille eines jiingeren Geometers, des Herro Dr. Rosemann, in der Anlage und den Einzelheiten einer griindlichen Neubearbeitung zu unterziehen. Diese Arbeit erwies sich als langwieriger wie urspriing- lich geschatzt. Klein selbst konnte ihren AbschluB nicht mehr erleben. Zwar hatte er in tagli...
This volume contains the proceedings of the Conference on Conformal Dynamics and Hyperbolic Geometry, held October 21-23, 2010, in honor of Linda Keen's 70th birthday. This volume provides a valuable introduction to problems in conformal and hyperbolic geometry and one dimensional, conformal dynamics. It includes a classic expository article by John Milnor on the structure of hyperbolic components of the parameter space for dynamical systems arising from the iteration of polynomial maps in the c...
Metrical and Dynamical Aspects in Complex Analysis (Lecture Notes in Mathematics, #2195)
The central theme of this reference book is the metric geometry of complex analysis in several variables. Bridging a gap in the current literature, the text focuses on the fine behavior of the Kobayashi metric of complex manifolds and its relationships to dynamical systems, hyperbolicity in the sense of Gromov and operator theory, all very active areas of research. The modern points of view expressed in these notes, collected here for the first time, will be of interest to academics working in t...
Rigid Local Systems. (AM-139) (Annals of Mathematics Studies, #139)
by Nicholas M. Katz
Locally Mixed Symmetric Spaces (Springer Monographs in Mathematics)
by Bruce Hunt
What do the classification of algebraic surfaces, Weyl's dimension formula and maximal orders in central simple algebras have in common? All are related to a type of manifold called locally mixed symmetric spaces in this book. The presentation emphasizes geometric concepts and relations and gives each reader the "roter Faden", starting from the basics and proceeding towards quite advanced topics which lie at the intersection of differential and algebraic geometry, algebra and topology.Avoiding t...
A Gyrovector Space Approach to Hyperbolic Geometry (Synthesis Lectures on Mathematics and Statistics)
by Abraham Ungar
The mere mention of hyperbolic geometry is enough to strike fear in the heart of the undergraduate mathematics and physics student. Some regard themselves as excluded from the profound insights of hyperbolic geometry so that this enormous portion of human achievement is a closed door to them. The mission of this book is to open that door by making the hyperbolic geometry of Bolyai and Lobachevsky, as well as the special relativity theory of Einstein that it regulates, accessible to a wider audie...
In the 1880s, over fifty years after the discovery of the hyperbolic plane, Poincare pointed out that this plane provides a very useful context for describing the properties of the solutions of an important class of differential equations. Topics include Euclidean rigid motions, inversions, Euclidea
"...a blend of erudition (fascinating and sometimes obscure historical minutiae abound), popularization (mathematical rigor is relegated to appendices) and exposition (the reader need have little knowledge of the fields involved) ...and the illustrations include many superb examples of computer graphics that are works of art in their own right." Nature
This book is based on the experience of teaching the subject by the author in Russia, France, South Africa and Sweden. The author provides students and teachers with an easy to follow textbook spanning a variety of topics on tensors, Riemannian geometry and geometric approach to partial differential equations. Application of approximate transformation groups to the equations of general relativity in the de Sitter space simplifies the subject significantly.
Non-Euclidean Geometry for Babies (Math for Babies, #1)
by Fred Carlson