Compact Manifolds with Special Holonomy (Oxford Mathematical Monographs)
by Dominic David Joyce
The book starts with a thorough introduction to connections and holonomy groups, and to Riemannian, complex and Kähler geometry. Then the Calabi conjecture is proved and used to deduce the existence of compact manifolds with holonomy SU(m) (Calabi-Yau manifolds) and Sp(m) (hyperkähler manifolds). These are constructed and studied using complex algebraic geometry. The second half of the book is devoted to constructions of compact 7- and 8-manifolds with the exceptional holonomy groups 92 and...
Non-Euclidean Geometries (Mathematics and Its Applications, #581)
by J nos Bolyai, A Pr kopa, and Emil Moln r
"From nothing I have created a new different world," wrote Janos Bolyai to his father, Wolgang Bolyai, on November 3, 1823, to let him know his discovery of non-Euclidean geometry, as we call it today. The results of Bolyai and the co-discoverer, the Russian Lobachevskii, changed the course of mathematics, opened the way for modern physical theories of the twentieth century, and had an impact on the history of human culture. The papers in this volume, which commemorates the 200th anniversary of...
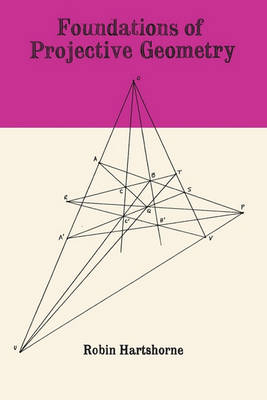
Vorlesungen uber Nicht-Euklidische Geometrie (Grundlehren der Mathematischen Wissenschaften, #26)
by Felix Klein
Als Felix Klein den Plan faBte, die wichtigsten seiner autogra- phierten Vorlesungen im Druck erscheinen zu lassen, gedachte er, mit der Nichteuklidischen Geometrie zu beginnen und den alten Text zu- vor mit Hille eines jiingeren Geometers, des Herro Dr. Rosemann, in der Anlage und den Einzelheiten einer griindlichen Neubearbeitung zu unterziehen. Diese Arbeit erwies sich als langwieriger wie urspriing- lich geschatzt. Klein selbst konnte ihren AbschluB nicht mehr erleben. Zwar hatte er in tagli...
This volume contains the proceedings of the Conference on Conformal Dynamics and Hyperbolic Geometry, held October 21-23, 2010, in honor of Linda Keen's 70th birthday. This volume provides a valuable introduction to problems in conformal and hyperbolic geometry and one dimensional, conformal dynamics. It includes a classic expository article by John Milnor on the structure of hyperbolic components of the parameter space for dynamical systems arising from the iteration of polynomial maps in the c...
Metrical and Dynamical Aspects in Complex Analysis (Lecture Notes in Mathematics, #2195)
The central theme of this reference book is the metric geometry of complex analysis in several variables. Bridging a gap in the current literature, the text focuses on the fine behavior of the Kobayashi metric of complex manifolds and its relationships to dynamical systems, hyperbolicity in the sense of Gromov and operator theory, all very active areas of research. The modern points of view expressed in these notes, collected here for the first time, will be of interest to academics working in t...
Rigid Local Systems. (AM-139) (Annals of Mathematics Studies, #139)
by Nicholas M. Katz
Equations in Mathematical Physics (Modern Birkhauser Classics)
by Victor P. Pikulin, Stanislav Pohazaev, and S. Pohozaev
Mathematical modeling and numerical simulation in fluid mechanics are topics of great importance both in theory and technical applications. The present book attempts to describe the current status in various areas of research. The 10 chapters, mostly survey articles, are written by internationally renowned specialists and offer a range of approaches to and views of the essential questions and problems. In particular, the theories of incompressible and compressible Navier-Stokes equations are con...
Elementare Differentialgeometrie (de Gruyter Studium)
by Christian Bar
Global Nonlinear Stability of Schwarzschild Spacetime under Polarized Perturbations (Annals of Mathematics Studies)
by Jeremie Szeftel and Sergiu Klainerman
Essential mathematical insights into one of the most important and challenging open problems in general relativity—the stability of black holesOne of the major outstanding questions about black holes is whether they remain stable when subject to small perturbations. An affirmative answer to this question would provide strong theoretical support for the physical reality of black holes. In this book, Sergiu Klainerman and Jérémie Szeftel take a first important step toward solving the fundamental b...
A Gyrovector Space Approach to Hyperbolic Geometry (Synthesis Lectures on Mathematics and Statistics)
by Abraham Ungar
The mere mention of hyperbolic geometry is enough to strike fear in the heart of the undergraduate mathematics and physics student. Some regard themselves as excluded from the profound insights of hyperbolic geometry so that this enormous portion of human achievement is a closed door to them. The mission of this book is to open that door by making the hyperbolic geometry of Bolyai and Lobachevsky, as well as the special relativity theory of Einstein that it regulates, accessible to a wider audie...
In the 1880s, over fifty years after the discovery of the hyperbolic plane, Poincare pointed out that this plane provides a very useful context for describing the properties of the solutions of an important class of differential equations. Topics include Euclidean rigid motions, inversions, Euclidea